
小概率事件原则是概率论中的一个基本且实用的原理。为便于读者理解并掌握这一原理,先看一个例子。
例1:某工厂每天分三批包装产品,规定每批产品的次品率必须低于1%才能出厂。若产品符合出厂要求,问从三批产品中各任抽取一件,抽到的三件产品中有0,1,2,3件次品的概率各是多少?若某日用上述方法抽查到了次品,问该日产品能否出厂?
解:把从三批产品中各抽取一件看作三次独立试验,于是问题可归结为贝努利概型。若产品符合要求,则p=0.01, q=1-p=0.99.故抽三件产品恰有0件次品的概率为:

这是一个概率很小的事件。在概率论中我们称之为小概率事件(一般情况下,把概率在0.05以下的事件称为小概率事件)。所谓小概率事件,其核心意思是:如果一个事件发生的概率很小,那么在一次试验中,实际上可以看成不可能事件。
由此原理可知,小概率事件在一次试验中实际上是不可能发生的。如果在一次试验中,某个小概率事件竟然发生了,那么就认为这是一种反常现象。上面例1中,从三批产品中各抽一件至少抽到一件次品的概率为0.03,这是小概率事件,现在发生了,这只能说明该日产品的次品率不止0.01,故判断该日产品不能出厂。
下面我们再举几个有趣的例子,便于从中更好地理解这一推断原理是如何应用于实际的。
例2:某车间有12台车床,每台车床由于种种原因,有时需要开有时需要停。设各台车床的开或停是相互独立的,如果对于每一台车床而言,停车的概率是1/3,问车间里恰好有K台车床处于停车状态的概率是多少。
解:我们把观察12台车床的开停情况,看作是进行12次实验,由于各台车床的开与停是相互独立的,所以又可看作是12次独立实验。每次试验只有停或开两种可能结果,而停的概率p=1/3。故所求的概率为:
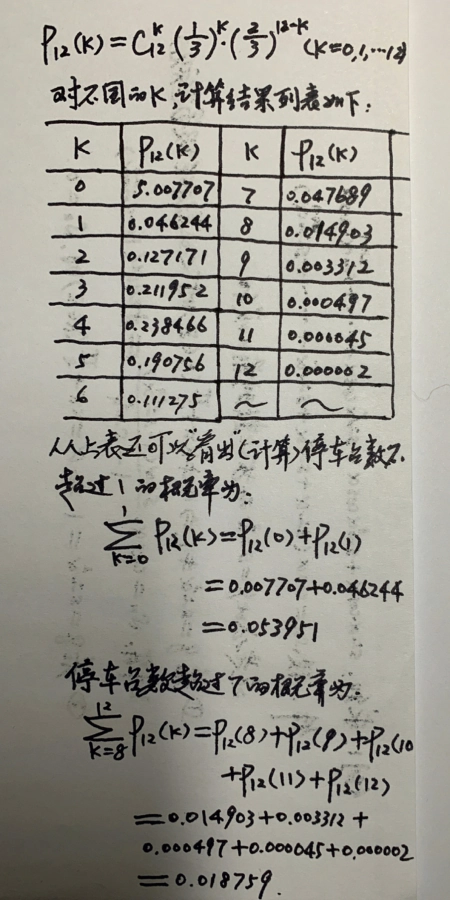
由此可见停车台数“不超过1”和停车台数“超过7”都是小概率事件。而这个结论是在停车概率假定等于三分之一的前提下得到的。于是我们可以利用这一推断通过实地观察,反过来检验停车概率假定为三分之一是否正确,如果观察的结果是12台车床中,发现停的台数的确不超过1(即只发现0台或1台车床停着)而出现这个情况是一个小概率事件,现在一次观察中竟然出现了,这是反常的。因此我们认为原来假定停车概率等于三分之一是偏大了,应予以纠正。如果观察的结果是12台车床有7台以上停着,这种情况的出现也是小概率事件,现在在一次观察中竟然出现了,这也是反常的。因此,我们有理由认为原来假定停车概率等于三分之一是偏小了,也应视具体情况予以纠正。







